沙之书(平子理沙书)

「“也许从现在开始，我可以每一秒数一个数字，每个数字都比之前数过的大，永远不结束。每数一个数字，我便离无穷大更近了一点。可是我再怎么数，也数不到无穷。我只要数出了那个数字，它就不是无穷。也许我的人生太短暂，但哪怕把这事儿交给脚下的石头来做，也数不到无穷。只要石头数出了那个数字，它就不是无穷。”」

本文所含故事约3000字，需要读者掌握高中程度的集合与映射概念即可。

从《沙之书》说起

——“他告诉我，他那本书叫‘沙之书’，因为那本书像沙一样，无始无终。”

《沙之书》是阿根廷作家博尔赫斯的短篇小说。其中描述了一本奇特的书，书的页码无穷无尽，既没有第一页，也没有最后一页；你翻开的每一页，之后都将再也见不到。当然，现实生活中并没有一本页数无穷的书，但是这样一本奇怪的书却给人们带来了巨大的遐想的空间。我们今天就来尝试分析一下沙之书的特点。

Page1

首先，我们可以从日常生活中书的特征总结出一些规律。如果总是假设纸的厚度相同，那么页数多的那一本也就更厚一些。直观地来看，厚度反映了书的页数。如果两本书一样厚，我们可以做一件有趣的事，把两本书的纸页一张一张地插起来，每一页都会和另一本的一页面对面贴着。警告：这可能会导致两本书在大气压下无法分开。

博尔赫斯面对沙之书，做了一件有趣的事情。“我发现每隔两千页有一帧小插画。我用一本有字母索引的记事簿把它们临摹下来。簿子不久就用完了。插画没有一张重复。” 现在我们做一个试验，把这个记事簿和沙之书插在一起，把相同的插画一张一张贴在一起。于是，沙之书中就会有这样的页面：没有记事簿的页面和它贴在一起。按照我们之前的说法，沙之书就比这个记事簿厚。日常的记事簿，不管有多少页，它的页数总是有限的。于是我们可以说，沙之书比任意一本页数有限的书都要厚。进一步，如果我们做出一本页数和自然数一样多的书，沙之书至少和它一样厚。

一本页数和自然数一样的书？事情突然数学起来。我还以为是一篇文学系的推送。是的，虽然现实中这样的书不存在，但在数学的角度，这其实并不难想象。正常的书都会有页码编号。我们现在提到的页数和自然数一样多的书，就刚好用掉了所有的自然数作为页码编号，不多也不少。你要是说出任何一个自然数，都能在这样一本书里找到以这个数为页码的那一面。

为了做这篇推送，小编我专门去希尔伯特的图书馆借了这本页数和自然数一样多的书（不妨称之为自然书），和其他几本书回来。

第一本书是记载了所有的完全平方数，按照顺序，每一页上都写了一个完全平方数：0,1,4,9,16……如果把它记载n^2的那一页和自然书的写有n的那一页插在一起，我们很高兴地发现，这两本书刚好可以面对面贴在一起。也就是说，两本书其实一样厚！

第二本书记载了所有的2的幂次，每一页上按顺序书写了一个2的幂次的数：1,2,4,8……同样地，把它记载2^n的一页和自然书的写有n的那一页贴在一起，又推出了两本书是一样厚的！

Page2

事情可真是奇怪，如果你在贴书的时候让这本书记载2^n 的一页和自然书的写有2^n 的一页贴在一起，也就是说，让这本书每两页之间有不止一张自然书的书页，可能会误以为这两本书不一样厚！

第三本书是一本记载所有正有理数的书。每一页上都记载了一个既约分数m/n，按照m+n和分数的大小从小到大排列。比如1/4排在2/3前面，2/3又排在3/4前面。你可能会问，为什么是m+n呢？其实很简单，m+n固定的既约分数总是数量有限的。而且这样做我们可以给出一个估计：

每一个正有理数m/n都可以在第[(m+n)(m+n+1)/2]+2019页之前找到（其实我不知道这个数到底在哪，所以不妨把数字放大一点）。

Page3

为了更具体一点，第三本书的前几页是这样的：

直观来想，这第三本书总该比那本自然书要厚。可事实却是，这两本书还是一样厚。道理很简单，我们把第三本书的第n页和自然书写有n的那一页贴在一起就完事了。关键在于，我们能够把所有正有理数不遗漏地排成一个数列{Xn}(n属于自然数)。

这似乎说明这本自然书与我们的常识并不大相同。第一第二本书看似内容比自然书少，第三本书看似内容比自然书多，他们却都一样厚。如果自然书的页码是有限多的，那这样的事情一定不会发生。但问题在于，这本书的页码无穷无尽。

第四本书就有些夸张了，它记载了[0,1]中的所有实数。这一次，我没有找到任何一种方法，使第四本书和自然书的书页能一页对着一页插在一起。这第四本书的书页似乎多得让人头昏脑胀。当然，没有找到方法的原因有两种，一种是方法不存在，一种是我不够聪明。我在很久之后才知道，这样的方法确实不存在。但这并不能否认我不够聪明。

Page4

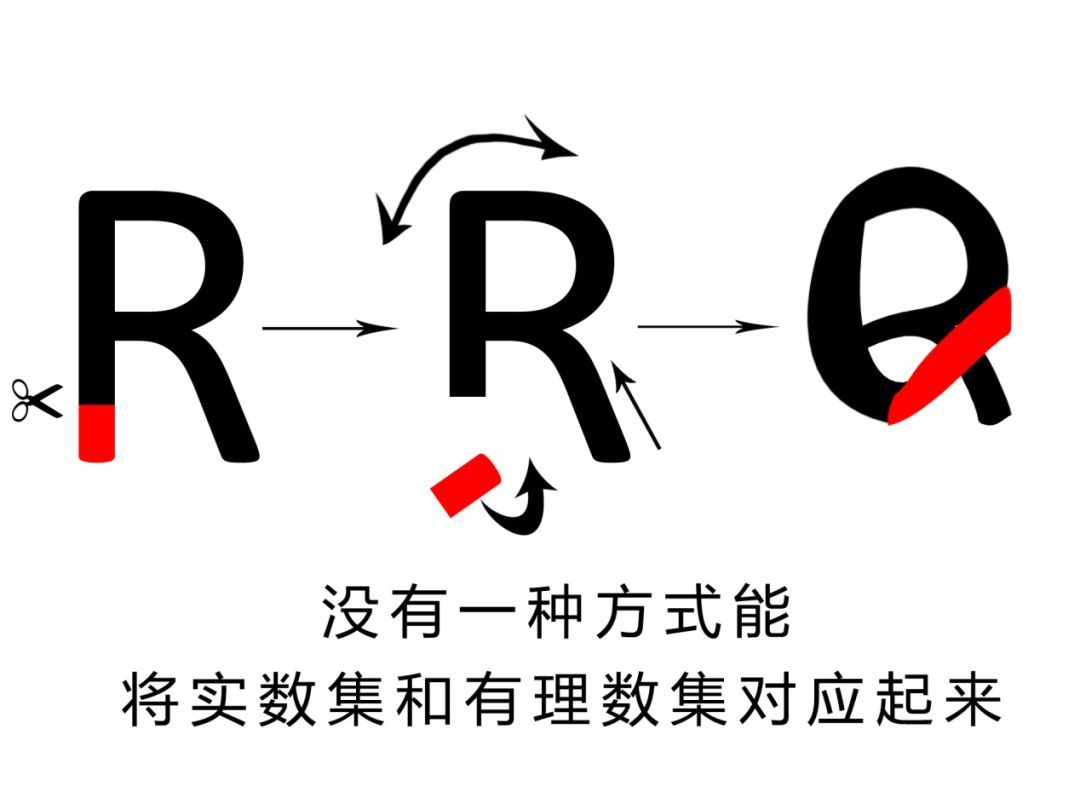
我当时借了这几本书后，去问管理员希尔伯特：“你们这里最厚的书放在什么地方呢？”希尔伯特哈哈大笑，说：“你到顶层的文印室去找康托尔，他会告诉你事实的。”

于是我就去了一趟文印室，发现康托尔坐在一台奇怪的机器旁边工作。康托尔告诉我，这是一台印刷机，你放一本书进去，就可以印一本书出来。于是我好奇地把自然书放了进去，不一会儿功夫，出来一本厚得多的书。我比了比，似乎和第四本书差不多厚。

康托尔解释道，这台印刷机会根据放进去的书，重新打印一本新的书出来。这本新的书中，每一页都记载着原书的某一部分，每两页记载的东西不重样。而原书的任何一部分，都会在某一页当中。

Page5

为了让我更明白一点，康托尔翻到了某一页，这一页记载着“自然书全部的书页”，也就是整本自然书。接着，则是记着“全体记有偶数的书页”的书页，“全体记有奇数的书页” 的书页，“全体记有质数的书页” 的书页。还有一些书页，上面只印有有限多的自然书的书页——这些都是自然书的一部分。当然，更有特殊的一页，那上面什么也没记。

“这似乎没有什么奇怪的。”我说。康托尔摇摇头：“不不不，这样每次印出来的书都比之前的书要厚。”

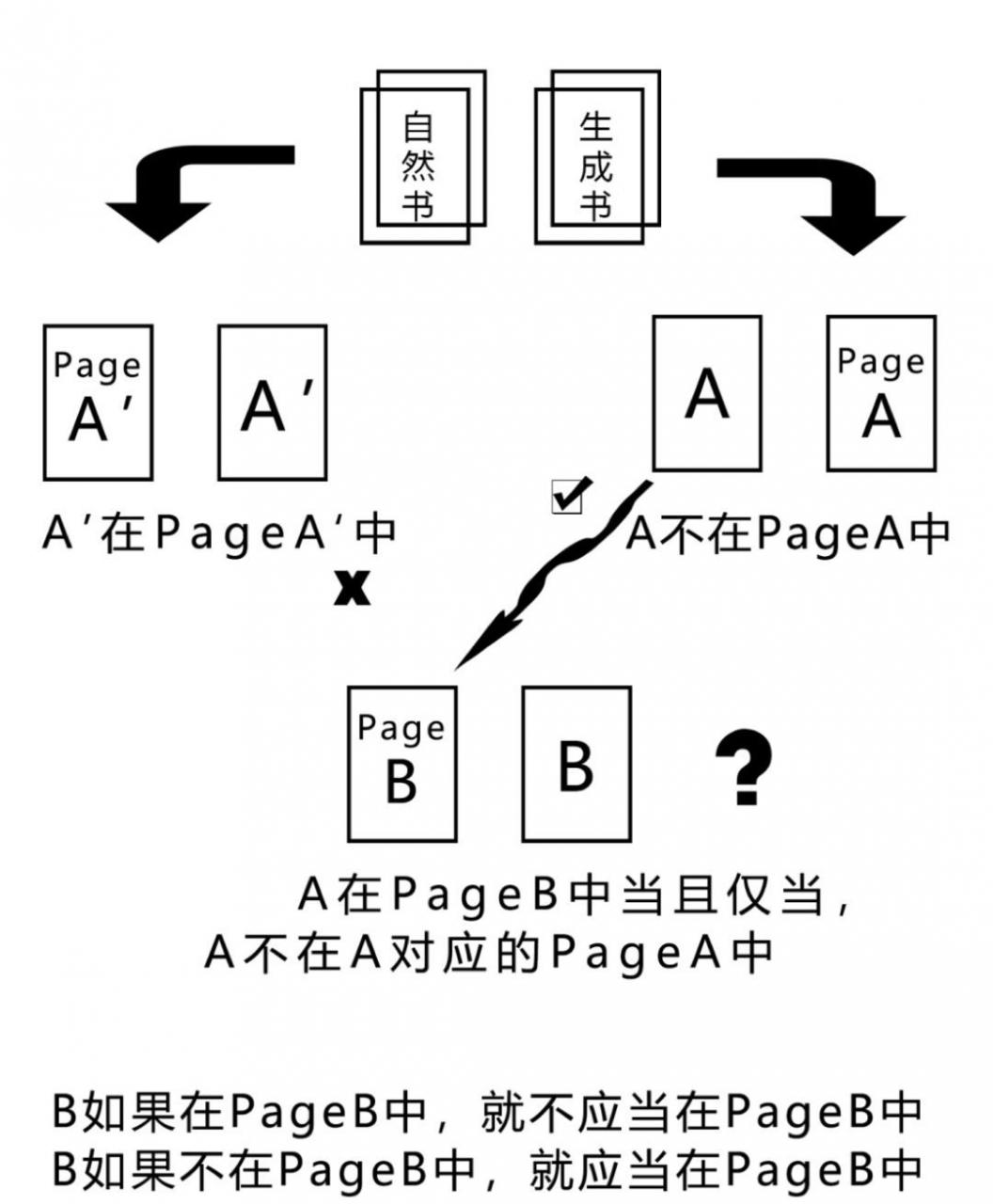
原来，如果原书和印出来的书可以一页贴着一页插在一起的话，原书每一页A都会和印出来的书某一页，不妨记为PageA，贴在一起。A可能印在PageA上，也可能并不在。我们把所有的不在PageA中的原书中的那些书页A都放在一起，这些书页全体也是原书的一部分，所以它们被印在了印出来的书的某一页PageB上。与PageB对应的就是原书的某一页，B。现在，B有没有被印在PageB中呢？如果，它在PageB中，按照PageB的组成方式，B不在PageB中；反过来，B如果不在PageB中，它就应当在PageB中。这可太矛盾了！

我听完一顿分析，终于明白之后，感到了与博尔赫斯相同的绝望。这时希尔伯特上来了，看到我颓废的样子真的很靓仔，拍了拍我的肩膀，指了指墙角的一大堆书：“那些就是以前我们留下的实验品。我们并不会让他们上架给大家看。事实上，目前也没有人知道那些书写的是什么意思。现在我们收录的最厚的书，是那本记载着所有平面上曲线的书，它比你手上那本记载着[0,1]上全体实数的书还要厚一些。但是更厚的就没有了。”“所以，这纯粹只是一些我们的想象？”我说道。康托尔和希尔伯特摇了摇头，“不知道。也许是。”“所以我们要继续探索，即使可能什么都找不到。”两位数学家坚定的目光给了我继续学习的动力。我拾起一本书，看到了一张插画：一个钢笔绘制的铁锚，笔法笨拙，仿佛小孩画的。又翻了几页，其中一页印有一个面具。角上有个数字，现在记不清是多少，反正大到九次幂……

是啊，隐藏一片树叶的最好的地点是树林。这真的是沙之书最好的归宿……

供稿｜学术部

排版｜新媒体许雯颖